Academic, 2021
Visual Affordances for communicating Auction theory

Individual Project for CS-234R Networks and Crowds
HTML / CSS / JS

Introduction

The project acknowledges the barrier to entry for students enthusiastic about studying network and crowd models, the mathematical notation. For many, who either have to interact in these markets or wish to learn them, the sparse number of visualizations of some of the auction's mechanisms make it difficult for users to understand and then engage in bidding. The project looks at the possible affordances in visual notation, how this applies to a couple of standard auctions and how it could be extended to other auctions. Lastly, I present this to individuals unfamiliar with mathematics beyond high school to tease out some of the intuition behind some of the theorems we have studied (such as revenue equivalence). The outcome is anecdotal since it has not been studied with many individuals. Still, it shows promise since most of them were able to guess a very weak version of revenue equivalence.

The solution I presented here borrows extensively from the late 19th century as far as I can tell. During that time, the interval notation and the corresponding visuals associated with it were developed. L.A. Skornyakov, 2011 and Teruo Sunaga, 1958, have both made anecdotal notes to the development of the interval notation and the importance it had in the development of algebra and calculus, but it is hard to pin down the original creator of this idea. To condense the idea interval notation (Something that most of us are familiar with from High school) I present the following example (Borrowed from brilliant.org):

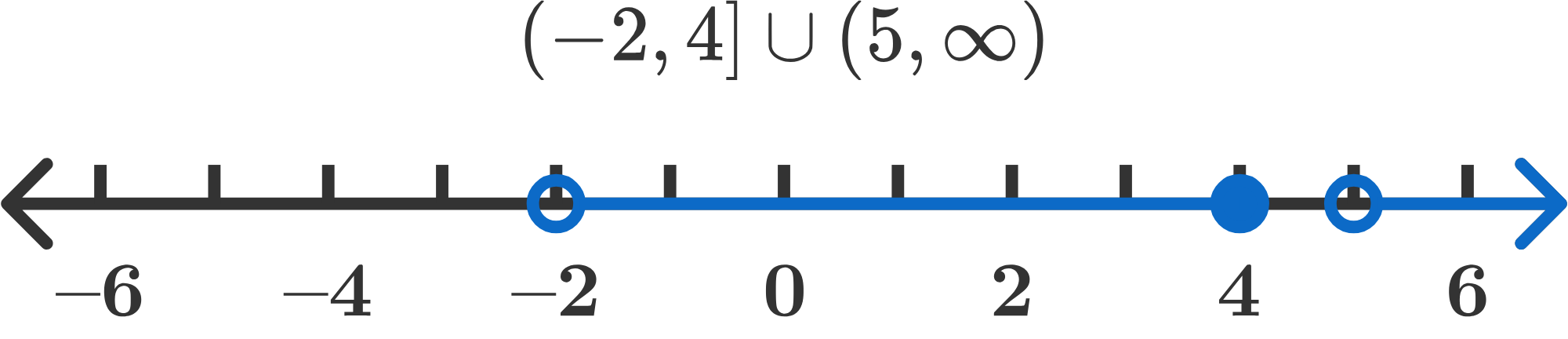
The notation here says that there is an interval from (excluding 2) 2 to (including 4) and the interval from (excluding) 5 to infinity. The notation is then represented on the number line, which makes the outcome visible and allows for visual understanding of the notation. Again, I would like to highlight that the above method only makes sense for communication to those unfamiliar with the communication of the models and not necessarily to solve these problems or to communicate with fellow researchers working on this.

Proposed Visuals

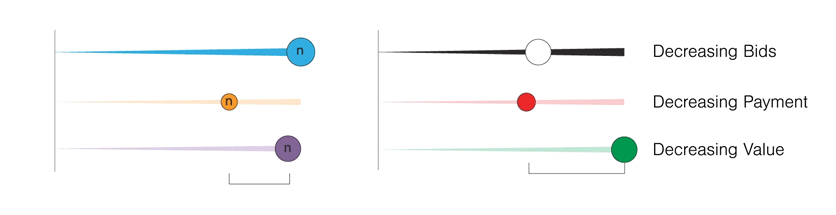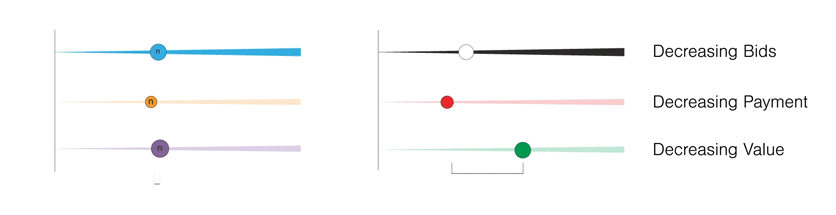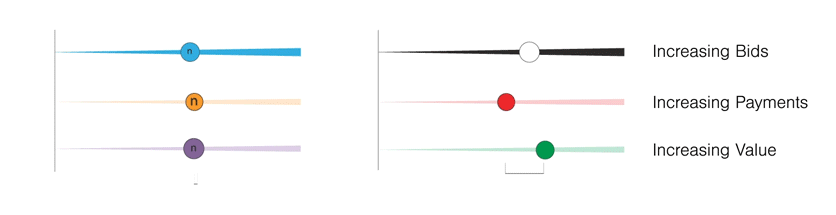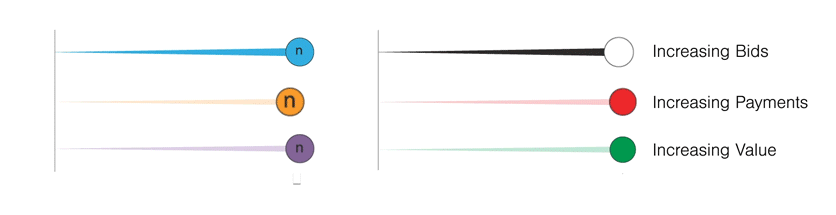
The interval notatation allows us to think about a range of inputs to be sliders that can be interacted with. This would mean that there are possibly infinite combinations of these sliders. And, some setting of these sliders to some specific value shall have a specific property. Are they the equilibria or not – can that bid payment strategy allow for some of these states to occur or not etc. Keeping the idea of sliders in mind, I shall present what an agent is in an alternate notation – more along the lines of intervals.

Here the blue line which is increasing in width would be the agent's bid value. In the first case, it is increasing as the value also increases, but this does not have to be the case, as illustrated in the adjacent visual where it increases and then decreases in its bid value.Similarly, we can define the possible range of payment the agent has to make:

Again, in the first example, the payment value increases with increasing value. In the second case, the payment increases to a certain value and then decreases with increasing value. Lastly, the agent is bidding for a certain good or service. This also has a certain value that the agent has for it.

These three sliders together describe an agent. Hence, every agent can make a bid based on their bid value slider, make a payment based on their payment value slider, and have a value derived after the end of the auction. The following figure captures this definition of the nth agent (denoted by the 'n'). Lastly, for the sake of completeness and for making explanations easier, it makes sense to introduce the idea of you, the reader, as a player and explain the behaviour and the outcomes of the auctions if you were participating in it in the first person. The notation is the same, the only difference being the colours. These three sliders together describe an agent. Hence, every agent can make a bid based on their bid value slider, make a payment based on their payment value slider, and have a value derived after the end of the auction.

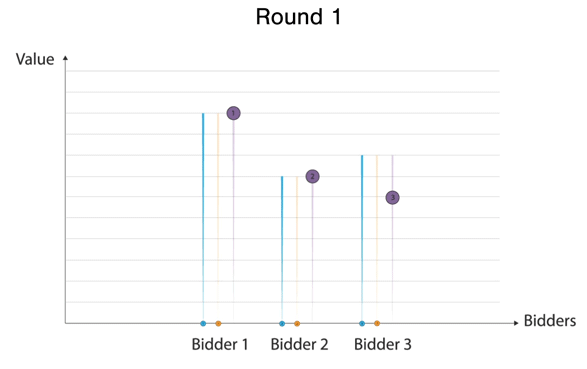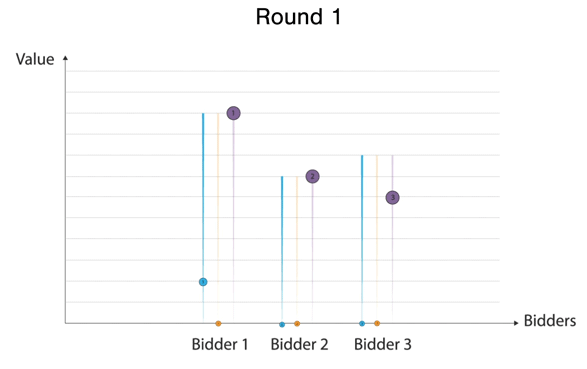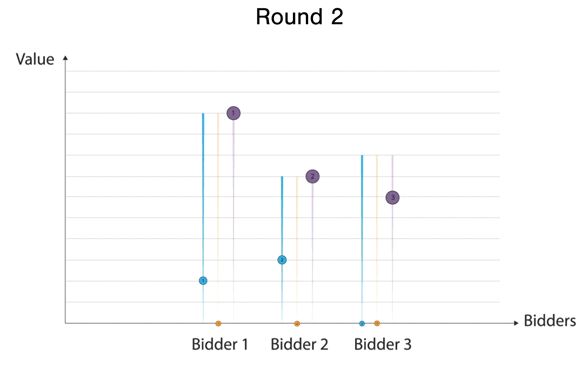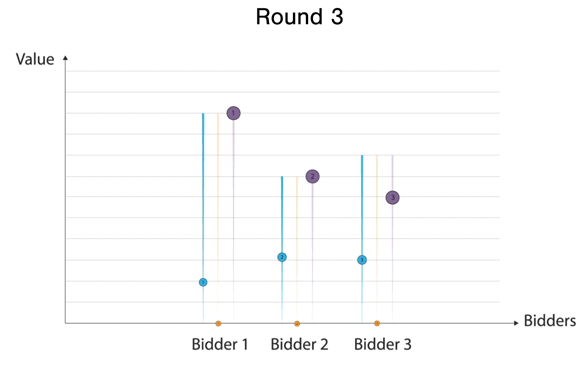
An ascending auction with single item

In the notation illustrated consider the following auction play out - Round 1 Bidder 1 places a bid; Round 2, Bidder 2 outbids bidder 1. In Round 3, Bidder 3 outbids them all. Round 4 results in Bidder 1 taking the lead again. Round 5 results in Bidder 2 taking the lead again. Note that Bidder 3 can outbid them all but is indifferent and disengages given the value he has. Finally, In round 6, Bidder 1 outbids Bidder 2 and Bidder 2 disengages since Bidder 1 has a higher bid than their value.

VCG with a single item

Now I shall introduce a similar idea but in the context of VCG auction with a single good. The payment scheme is that the highest bidder wins the good at the second-highest bid. All the bids are sealed bids, and only the auctioneer knows what the values are. The setup is shown below :

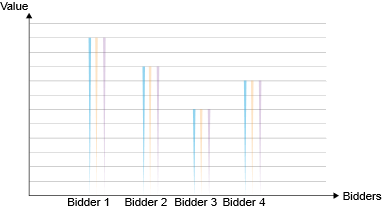
Here there are four bidders with varying valuations and payments. Again, here I have assumed that the respective bids, payments and received values increase with the increase in value.

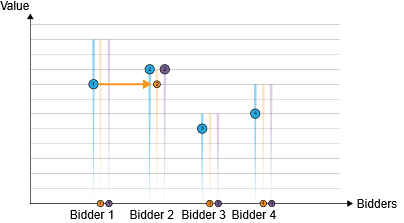
So let us say that the bidders randomly pick values and send them in. As illustrated above – what happens in this case? Well, Agent 2 has won the good at the highest at the second-highest bid, which was agent 2's bid. Now imagine you are also a part of this auction.

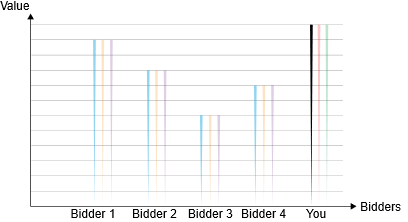
Your valuation and the possible payments that you could make are also shown here. So what do you do? You could bid any value, but let's assume that you don't do that; you bid the highest possible value for the product. In the worst case, you have to pay what you value it; in any other case, you will always pay a lesser amount of money to your value! Since you have won the good and you pay the second-highest bid, which is lower than yours. In short, the worst case is that you are indifferent, and otherwise, you keep getting greater than zero utility. Now, assuming that all the agents also figure this out – what happens as an outcome?

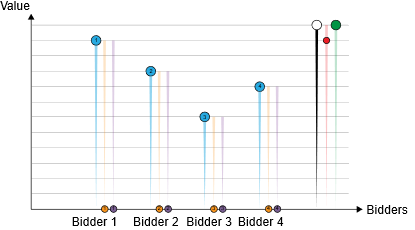
Here everyone bid their highest bid and so did you. Since you made the highest bid, you get the good at the second highest bid, which is agent 1's bid. A couple of more examples with VCG auctions and a single item:

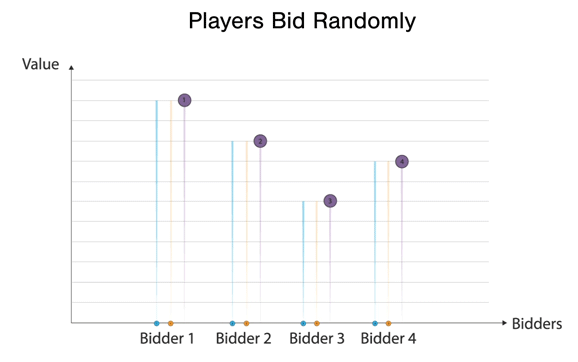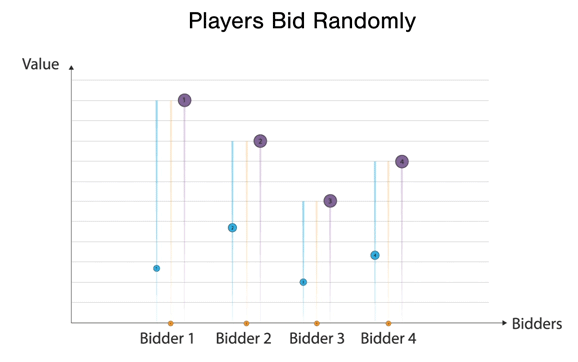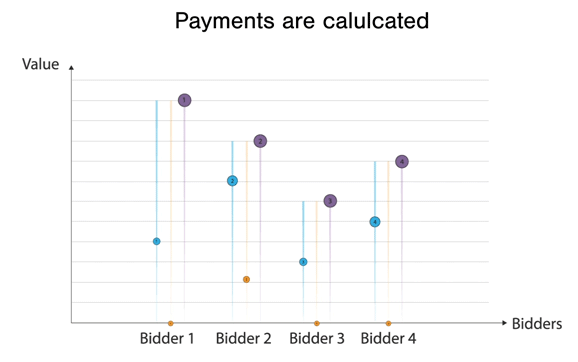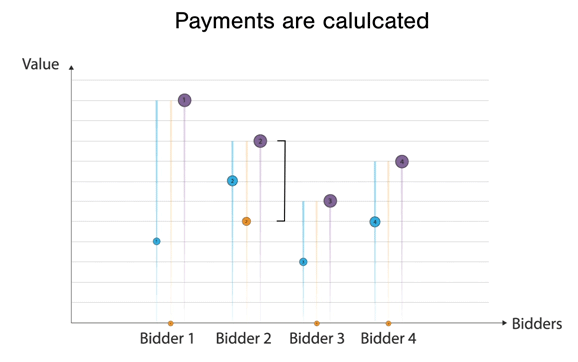
In this case, players bid randomly, and Bidder 2 wins the good at the second highest bid price, that of bidder 4. Another example of VCG with a single good:

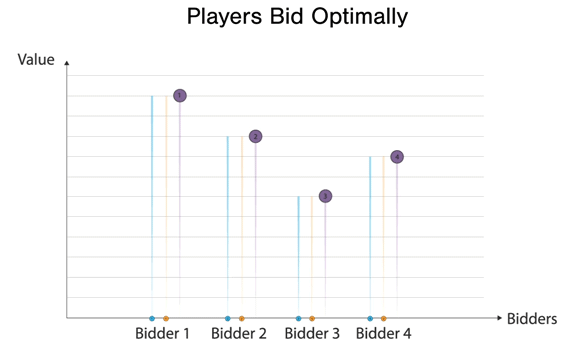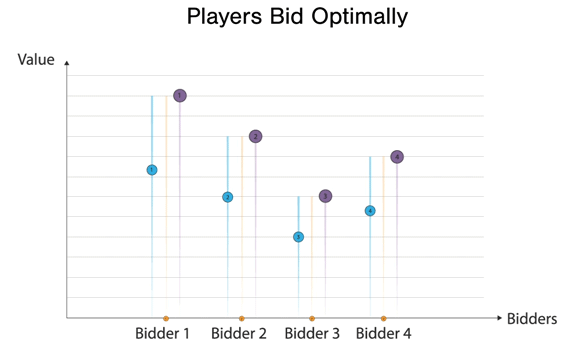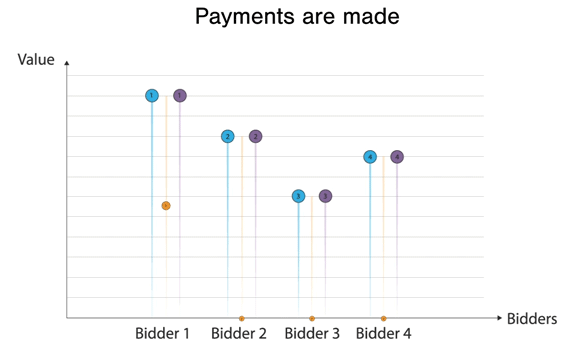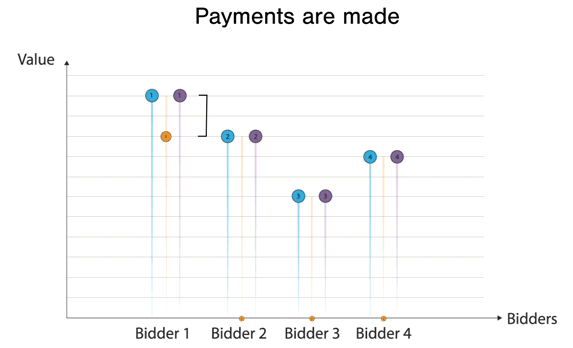
Here, the bidders are bidding optimally, and Bidder 1 wins the good at Bidder 2's bid. Moreover, to further highlight the example through an interactive example, please check this javascript app that I made:

VCG with multiple items

I shall be motivating multi-item VCG auctions with a contrived example of going on a tour of concerts as some musician. The cities are the edges in the graph below and visiting one city opens up the possibility to go to other linked cities. There is one key caveat, though; you must not go back to one of the cities you already visited (since you want to visit as many fans as possible and not appear preferential). You also want to have the longest trip ever so as to write about it in your new album. So being the music / CS / Economics virtuoso that you are, you decide to hold an auction where the cities participate and make bids to figure this out. We shall imagine this as a graph as that is what leads to the best possible visual analogy.

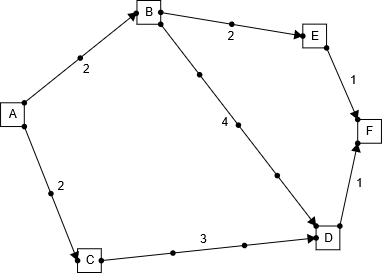
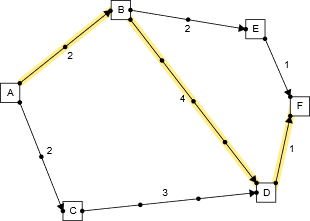
In the analogy above, the tour starts at A, and we can choose whatever set of paths leading us to F, which is when the tour ends. We don't know the whole graph of cities, but we do know for example, that state F can be reached only through E or D. All the host cities, i.e. agents report the bids they want you (as a dollar amount payment, this can be thought of as the revenue that you generate as tickets * attendance) then we want to figure out what is the best possible path that we should take. In this case, you take the longest route possible:

Now, suppose the agents make their time bids like so (in this case randomly) :

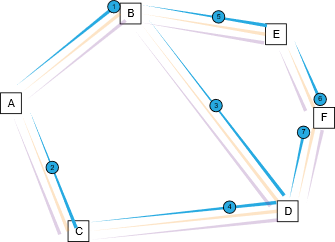
Now you as the market maker see only the reported bids and use that as a proxy for their value.

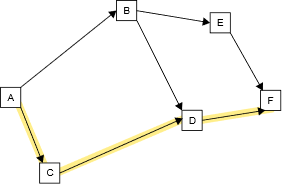
So we redraw the graph. Hence I want to maximize the time spent, the longest path from A to F is through C,D and I decide to take path ACDF.Now before we begin analyzing the truthfulness of the auction, let's visualize the payment rule of VCG in this case

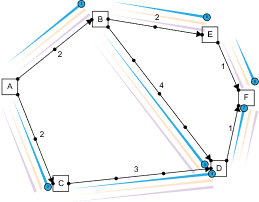
In this contrived setting, every city reports their bid (value) for hosting you. In this case, we shall look at city BD and figure out how much to charge them. Imagine a situation that city BD was not there. In the current setup path, ABDF is 7 units long.

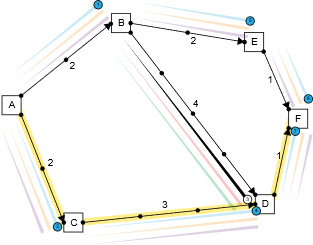
The next best path that you have is one through ACDF. Hence you should take that path which is 6 units long. Hence by existing BD has added in a value of 1. And that is how much BD should get paid. Let's use this to figure out how much everyone else has to pay, visualized in the following diagram:

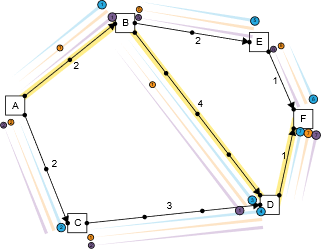
Now we shall look at what I would do if I were one of the agents and the best possible method of bidding. Again, the same setup and this time, I take agent CD from the last graph. I don't really know what cities that happen before me or after me are. Nor do I know what their valuations or payments are. To be honest, all I see is this:

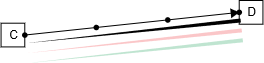
So I know that to go from activity state C to activity state D, and truthfully I can only do this in 3 units of ticket revenue. What happens if I overreport?

Overreporting results in me overshooting the target. Moreover, It is not in my best interest to do that. Since the more I add to the path length, the more I add to the payment, as we saw before. This would happen since the payment I make is the value that I generate over the other paths, overreporting increases that. So should I under-report?

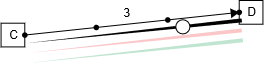
Underreporting would mean that I don't deliver the best possible experience and that other agents have more value get picked up as the market maker. So it wouldn't make sense to underreport either.I thus report the value truthfully. And all other agents must also come to the same logical conclusion and report their values truthfully. And this is the dominant strategy.

Other inferences that we can draw from this method of representation

This manner of representation also makes certain theorems a little more clear—for example, revenue equivalence in the ascending auction and the second price auction. The winners are the same, and as I make the minimum amount of bid arbitrarily small, the auctions as conducted in ascending and single item, VCG would yield the same outcome at the same price. The envelope theorem says, "in a certain sense, changes in the optimizer of the objective do not contribute to the change in the objective function". Now, this must make sense since if I arrive at the same outcome, the mechanism that I used to optimize it didn't make much of a difference, as what we see in the ascending auction where we optimized from the bottom, a descending auction optimizing from the top or the second price auction. Although in no way are these rigorous, it does motivate some of the intuition behind these theorems. Lastly, I could imagine extending this to revenue optimal and Myerson auctions and mechanisms. I perform some transformation to all the lengths, construct a new graph (or a distorted graph and then) generate the outcome.